FIFA 20: explain default vs tuned model with dalex

imports

In [1]:
import dalex as dx 

import numpy as np
import pandas as pd

from lightgbm import LGBMRegressor
from sklearn.model_selection import train_test_split
from sklearn.model_selection import RandomizedSearchCV

import warnings
warnings.filterwarnings('ignore')

import plotly
plotly.offline.init_notebook_mode()
In [2]:
dx.__version__
Out[2]:
'1.7.0'

load data

Load fifa, the preprocessed players_20 dataset. It contains 5000 'overall' best players and 43 columns. These are:

  • short_name (index)
  • nationality of the player (not used in modeling)
  • overall, potential, value_eur, wage_eur (4 potential target variables)
  • age, height, weight, attacking skills, defending skills, goalkeeping skills (37 variables)

It is advised to leave only one target variable for modeling.

In [3]:
data = dx.datasets.load_fifa()
In [4]:
data.head(10)
Out[4]:
nationality overall potential wage_eur value_eur age height_cm weight_kg attacking_crossing attacking_finishing ... mentality_penalties mentality_composure defending_marking defending_standing_tackle defending_sliding_tackle goalkeeping_diving goalkeeping_handling goalkeeping_kicking goalkeeping_positioning goalkeeping_reflexes
short_name
L. Messi Argentina 94 94 565000 95500000 32 170 72 88 95 ... 75 96 33 37 26 6 11 15 14 8
Cristiano Ronaldo Portugal 93 93 405000 58500000 34 187 83 84 94 ... 85 95 28 32 24 7 11 15 14 11
Neymar Jr Brazil 92 92 290000 105500000 27 175 68 87 87 ... 90 94 27 26 29 9 9 15 15 11
J. Oblak Slovenia 91 93 125000 77500000 26 188 87 13 11 ... 11 68 27 12 18 87 92 78 90 89
E. Hazard Belgium 91 91 470000 90000000 28 175 74 81 84 ... 88 91 34 27 22 11 12 6 8 8
K. De Bruyne Belgium 91 91 370000 90000000 28 181 70 93 82 ... 79 91 68 58 51 15 13 5 10 13
M. ter Stegen Germany 90 93 250000 67500000 27 187 85 18 14 ... 25 70 25 13 10 88 85 88 88 90
V. van Dijk Netherlands 90 91 200000 78000000 27 193 92 53 52 ... 62 89 91 92 85 13 10 13 11 11
L. Modric Croatia 90 90 340000 45000000 33 172 66 86 72 ... 82 92 68 76 71 13 9 7 14 9
M. Salah Egypt 90 90 240000 80500000 27 175 71 79 90 ... 77 91 38 43 41 14 14 9 11 14

10 rows × 42 columns

Divide the data into variables X and a target variable y. Here we will be predicting the value of the best players.

In [5]:
X = data.drop(["nationality", "overall", "potential", "value_eur", "wage_eur"], axis = 1)
y = data['value_eur']

The target variable is skewed so we transform it with log for a better fit.

In [6]:
ylog = np.log(y)

import matplotlib.pyplot as plt
plt.hist(ylog, bins='auto')
plt.title("ln(value_eur)")
plt.show()
No description has been provided for this image

Split the data into train and test.

In [7]:
X_train, X_test, ylog_train, ylog_test, y_train, y_test = \
    train_test_split(X, ylog, y, test_size=0.25, random_state=4)

create a default boosting model

In [8]:
gbm_default = LGBMRegressor()

gbm_default.fit(X_train, ylog_train)

[LightGBM] [Info] Auto-choosing col-wise multi-threading, the overhead of testing was 0.000364 seconds.
You can set `force_col_wise=true` to remove the overhead.
[LightGBM] [Info] Total Bins 2596
[LightGBM] [Info] Number of data points in the train set: 3750, number of used features: 37
[LightGBM] [Info] Start training from score 15.433596
Out[8]:
LGBMRegressor()
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

create a tuned model

In [9]:
gbm_default._estimator_type
Out[9]:
'regressor'
In [10]:
#:# hp tuning
estimator = LGBMRegressor(n_jobs = -1)
param_test = {
    'n_estimators': list(range(201,1202,50)),
    'num_leaves': list(range(6, 42, 5)),
    'min_child_weight': [1e-3, 1e-2, 1e-1, 15e-2],
    'learning_rate': [1e-3, 1e-2, 1e-1, 15e-2]
}

rs = RandomizedSearchCV(
    estimator=estimator, 
    param_distributions=param_test, 
    n_iter=100,
    cv=4,
    random_state=1
)

# rs.fit(X, ylog)
# print('Best score reached: {} with params: {} '.format(rs.best_score_, rs.best_params_))
In [11]:
#:# best parameters after 100 iterations
best_params = {'num_leaves': 6,
               'n_estimators': 951,
               'min_child_weight': 0.1,
               'learning_rate': 0.15}
In [12]:
gbm_tuned = LGBMRegressor(**best_params)
gbm_tuned.fit(X_train, ylog_train)

[LightGBM] [Info] Auto-choosing col-wise multi-threading, the overhead of testing was 0.000422 seconds.
You can set `force_col_wise=true` to remove the overhead.
[LightGBM] [Info] Total Bins 2596
[LightGBM] [Info] Number of data points in the train set: 3750, number of used features: 37
[LightGBM] [Info] Start training from score 15.433596
Out[12]:
LGBMRegressor(learning_rate=0.15, min_child_weight=0.1, n_estimators=951,
              num_leaves=6)
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

create explainers for the models

We aim to see real values of the target variable in the explanations (not log). Therefore, we need to make a custom predict_function.

In [13]:
def predict_function(model, data):
    return np.exp(model.predict(data))
In [14]:
exp_default = dx.Explainer(gbm_default, X_test, y_test,
                           predict_function=predict_function, label='default')
exp_tuned = dx.Explainer(gbm_tuned, X_test, y_test,
                         predict_function=predict_function, label='tuned')

Preparation of a new explainer is initiated

  -> data              : 1250 rows 37 cols
  -> target variable   : Parameter 'y' was a pandas.Series. Converted to a numpy.ndarray.
  -> target variable   : 1250 values
  -> model_class       : lightgbm.sklearn.LGBMRegressor (default)
  -> label             : default
  -> predict function  : <function predict_function at 0x29e725120> will be used
  -> predict function  : Accepts pandas.DataFrame and numpy.ndarray.
  -> predicted values  : min = 3.57e+05, mean = 7.12e+06, max = 8.12e+07
  -> model type        : regression will be used (default)
  -> residual function : difference between y and yhat (default)
  -> residuals         : min = -1e+07, mean = 2.12e+05, max = 2.43e+07
  -> model_info        : package lightgbm

A new explainer has been created!
Preparation of a new explainer is initiated

  -> data              : 1250 rows 37 cols
  -> target variable   : Parameter 'y' was a pandas.Series. Converted to a numpy.ndarray.
  -> target variable   : 1250 values
  -> model_class       : lightgbm.sklearn.LGBMRegressor (default)
  -> label             : tuned
  -> predict function  : <function predict_function at 0x29e725120> will be used
  -> predict function  : Accepts pandas.DataFrame and numpy.ndarray.
  -> predicted values  : min = 3.56e+05, mean = 7.12e+06, max = 9.51e+07
  -> model type        : regression will be used (default)
  -> residual function : difference between y and yhat (default)
  -> residuals         : min = -1.49e+07, mean = 2.11e+05, max = 2.41e+07
  -> model_info        : package lightgbm

A new explainer has been created!

introduction to the topic: Explanatory Model Analysis: Explore, Explain, and Examine Predictive Models

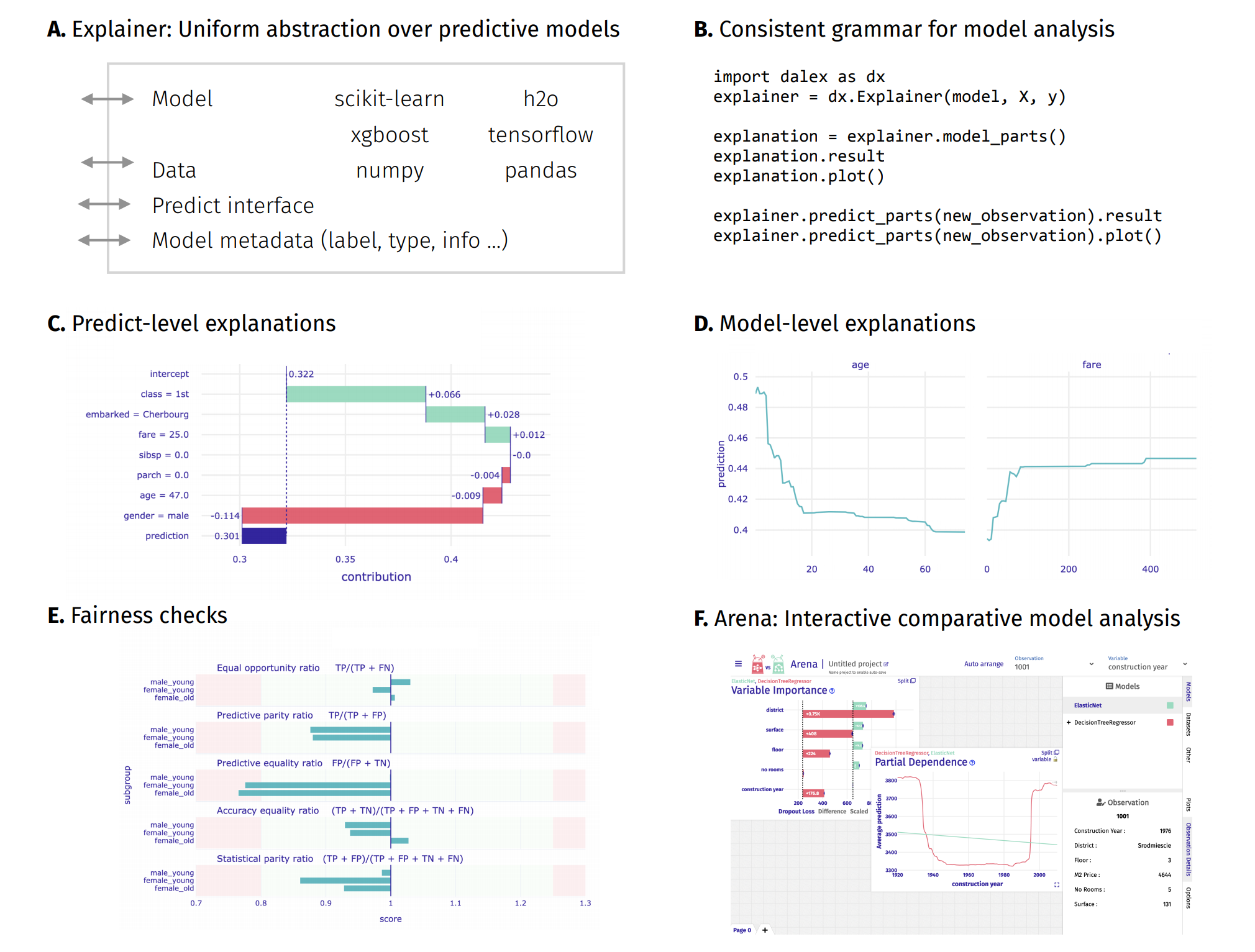
Above functionalities are accessible from the Explainer object through its methods.

Model-level and predict-level methods return a new unique object that contains the result attribute (pandas.DataFrame) and the plot method.

Model-level explanations

Model Performance

In [15]:
mp_default = exp_default.model_performance("regression")
mp_default.result
Out[15]:
mse rmse r2 mae mad
default 5.727888e+12 2.393301e+06 0.923228 1.209461e+06 651771.861674
In [16]:
mp_tuned = exp_tuned.model_performance("regression")
mp_tuned.result
Out[16]:
mse rmse r2 mae mad
tuned 4.117085e+12 2.029060e+06 0.944818 1.092173e+06 595137.6644
In [17]:
mp_default.plot(mp_tuned)

This are very big values so the difference on paper may be very subtle.

What are the differences between these two models? Let's find out.

Variable Importance

Customize the computation with parameters:

  • loss_function function to use for drop-out loss evaluation

  • B number of bootstrap rounds (e.g. 15 for slower computation but more stable results)

  • N number of observations to use (e.g. 500 for faster computation but less stable results)

  • variable_groups Dict of lists of variables. Each list is treated as one group. This is for testing joint variable importance

In [18]:
X.columns
Out[18]:
Index(['age', 'height_cm', 'weight_kg', 'attacking_crossing',
       'attacking_finishing', 'attacking_heading_accuracy',
       'attacking_short_passing', 'attacking_volleys', 'skill_dribbling',
       'skill_curve', 'skill_fk_accuracy', 'skill_long_passing',
       'skill_ball_control', 'movement_acceleration', 'movement_sprint_speed',
       'movement_agility', 'movement_reactions', 'movement_balance',
       'power_shot_power', 'power_jumping', 'power_stamina', 'power_strength',
       'power_long_shots', 'mentality_aggression', 'mentality_interceptions',
       'mentality_positioning', 'mentality_vision', 'mentality_penalties',
       'mentality_composure', 'defending_marking', 'defending_standing_tackle',
       'defending_sliding_tackle', 'goalkeeping_diving',
       'goalkeeping_handling', 'goalkeeping_kicking',
       'goalkeeping_positioning', 'goalkeeping_reflexes'],
      dtype='object')
In [19]:
variable_groups = {
    'age': ['age'],
    'body': ['height_cm', 'weight_kg'],
    'attacking': ['attacking_crossing',
       'attacking_finishing', 'attacking_heading_accuracy',
       'attacking_short_passing', 'attacking_volleys'],
    'skill': ['skill_dribbling',
       'skill_curve', 'skill_fk_accuracy', 'skill_long_passing',
       'skill_ball_control'],
    'movement': ['movement_acceleration', 'movement_sprint_speed',
       'movement_agility', 'movement_reactions', 'movement_balance'],
    'power': ['power_shot_power', 'power_jumping', 'power_stamina', 'power_strength',
       'power_long_shots'],
    'mentality': ['mentality_aggression', 'mentality_interceptions',
       'mentality_positioning', 'mentality_vision', 'mentality_penalties',
       'mentality_composure'],
    'defending': ['defending_marking', 'defending_standing_tackle',
       'defending_sliding_tackle'],
    'goalkeeping' : ['goalkeeping_diving',
       'goalkeeping_handling', 'goalkeeping_kicking',
       'goalkeeping_positioning', 'goalkeeping_reflexes']
}
In [20]:
vi_default = exp_default.model_parts(variable_groups=variable_groups, B=15, random_state=0)
vi_tuned = exp_tuned.model_parts(variable_groups=variable_groups, B=15)

Customize the plot with parameters:

  • vertical_spacing value between 0.0 and 1.0 (e.g. 0.15 for more space between the plots)

  • rounding_function rounds the contributions (e.g. np.round, np.rint, np.ceil)

  • digits (e.g. 2 for np.round, None for np.rint)

In [21]:
vi_default.plot(vi_tuned,
                max_vars=6, rounding_function=np.rint, digits=None, vertical_spacing=0.15)

Variables connected with body and power aren't important for these models. It is also true for goalkeeping. This might mean that goalkeepers predictions aren't accurate. The most important factors in predicting players value are skill, attacking and movement.

It seems like the default model is focusing on movement variables too much and doesn't find other variables so important, especially skill. The tuned model finds mentality and defending quite important. Next, we will examine these variables closer.

Aggregated Profiles

Choose a proper algorithm. The explanations can be calulated as Partial Dependence Profile or Accumulated Local Dependence Profile.

The key parameter is N number of observations to use (e.g. 800 for slower computation but more stable results).

Here we will use ale plots, which work better if the explanatory variables are correlated.

In [22]:
ale_default = exp_default.model_profile(type = 'accumulated', N=800, label='ale-default')

Calculating ceteris paribus: 100%|██████████| 37/37 [00:02<00:00, 15.16it/s]
Calculating accumulated dependency: 100%|██████████| 37/37 [00:02<00:00, 14.57it/s]
In [23]:
ale_tuned = exp_tuned.model_profile(type = 'accumulated', N=800, label='ale-tuned')

Calculating ceteris paribus: 100%|██████████| 37/37 [00:06<00:00,  5.48it/s]
Calculating accumulated dependency: 100%|██████████| 37/37 [00:02<00:00, 14.22it/s]
In [24]:
ale_default.plot(ale_tuned, variables = ['goalkeeping_positioning', 'power_stamina',
                                           'mentality_vision', 'defending_marking',
                                           'attacking_finishing', 'attacking_heading_accuracy',
                                           'attacking_short_passing', 'skill_ball_control'])

Overall, we can see that the tuned model is using more variables. Examples are defending_marking, goalkeeping_positioning, mentality_vision, power_stamina, skill_ball_control and attacking variables.

It also acts differently with variables like age and movement_reactions.

In [25]:
ale_default.plot(ale_tuned, variables = ['age', 'movement_reactions'])

Predict-level explanations

Variable Attribution

Choose a proper algorithm. The explanations can be calulated as Break Down, iBreakDown or Shapley Values.

For type='shap' the key parameter is B number of bootstrap rounds (e.g. 10 for faster computation but less stable results).

Let's find out what attributes to the value of the best players.

In [26]:
va = {'ibd':[], 'sh':[]}

for name in data.index[0:3]:
    player = X.loc[name,]
    
    ibd = exp_tuned.predict_parts(player, type='break_down_interactions', label=name)
    sh = exp_tuned.predict_parts(player, type='shap', B=10, label=name)
    
    va['ibd'].append(ibd)
    va['sh'].append(sh)
In [27]:
va['ibd'][0].plot(va['ibd'][1:3],
                  rounding_function=lambda x, digits: np.rint(x, digits).astype(int),
                  digits=None, max_vars=10)
In [28]:
va['sh'][0].plot(va['sh'][1:3],
                 rounding_function=lambda x, digits: np.rint(x, digits).astype(int),
                 digits=None, max_vars=10)

Looking at the Break Down plots, age and movement_ractions variables are standing out. Let's focus on them more.

Ceteris Paribus Profiles

In [29]:
cp = exp_tuned.predict_profile(X.iloc[2:3,],
                               variables=['age', 'movement_reactions'],
                               label=X.index[2]) # variables to calculate 

Calculating ceteris paribus: 100%|██████████| 2/2 [00:00<00:00, 548.42it/s]
In [30]:
cp.plot(size=3, title="What If? Neymar Jr") # larger width of the line and dot size & change title

Here we see how the prediction would change if Neymar Jr was younger/older or had lower movement_reactions.

Hover over all of the above plots for tooltips with more information.

Plots

This package uses plotly to render the plots:

Resources - https://dalex.drwhy.ai/python